Kelas XI IPA1
Program Linear: Menentukan Nilai Optimum Suatu Fungsi Objektif dengan Menggunakan Metode Uji Titik Pojok
Dalam pembahasan “Program Linear: Model Matematika” telah dibahas bagaimana memodelkan suatu permasalahan ke dalam model matematika. Dalam pembahasan tersebut diperoleh pemodelan sebagai berikut.
x + y ≤ 600,
6.000x + 5.000y ≤ 600.000,
Untuk x, y anggota bilangan cacah, x ≥ 0, y ≥ 0
Dari sistem pertidaksamaan tersebut akan dicari nilai-nilai x dan y yang menyebabkan fungsi f(x,y) = 500x + 600y bernilai maksimum. Bentuk umum dari fungsi tersebut adalah f(x, y) = ax + by. Fungsi yang akan dioptimumkan (maksimum atau minimum) ini kemudian disebut fungsi objektif. Untuk menentukan nilai optimum tersebut, dapat digunakan metode uji titik pojok.
Sebelum membahas metode uji titik pojok, sebaiknya kalian tahu mengenai nilai optimum. Nilai optimum dapat berupa nilai maksimum atau minimum, tergantung dari permintaan soal. Pada permasalahan ini yang diminta adalah nilai maksimum, sehingga kita akan mencari nilai-nilai x dan y yang menyebabkan fungsi objektif bernilai maksimum.
Metode Uji Titik Pojok
Untuk menentukan nilai optimum dengan menggunakan metode uji titik pojok, lakukan langkah-langkah berikut.
- Tentukan kendala-kendala dari permasalahan program linear yang dimaksud.
- Gambarlah daerah penyelesaian dari kendala-kendala dalam masalah program linear tersebut.
- Tentukan titik-titik pojok dari daerah penyelesaian itu.
- Substitusikan koordinat setiap titik pojok itu ke dalam fungsi objektif.
- Bandingkan nilai-nilai fungsi objektif tersebut. Nilai terbesar berarti menunjukkan nilai maksimum dari fungsi f(x, y), sedangkan nilai terkecil berarti menunjukkan nilai minimum dari fungsi f(x, y).
Untuk lebih memahami dalam menentukan nilai optimum suatu fungsi objektif dengan menggunakan metode uji pojok, perhatikan contoh soal berikut.
Contoh Soal
1. Suatu area parkir mempunyai luas . Luas rata-rata untuk mobil kecil dan mobil besar . Daya tampung daerah parkir maksimum 200 kendaraan. Biaya parkir mobil kecil Rp1.000,00/jam dan mobil besar Rp2.000,00/jam. Jika dalam satu jam daerah parkir terisi penuh dan tidak ada kendaraan yang pergi dan datang, maka penghasilan maksimum tempat parkir itu sebesar …
A. Rp176.000,00 D. Rp300.000,00
B. Rp200.000,00 E. Rp340.000,00
C. Rp260.000,00
A. Rp176.000,00 D. Rp300.000,00
B. Rp200.000,00 E. Rp340.000,00
C. Rp260.000,00
Penyelesaian
Misalkan berturut-turut menyatakan banyaknya mobil kecil dan mobil besar, maka dapat dibentuk model matematika berupa sistem pertidaksamaan linear sebagai berikut dengan memperhatikan tabel di bawah.
Fungsi objektif:
Gambarkan sistem pertidaksamaan linear di atas ke dalam sistem koordinat.
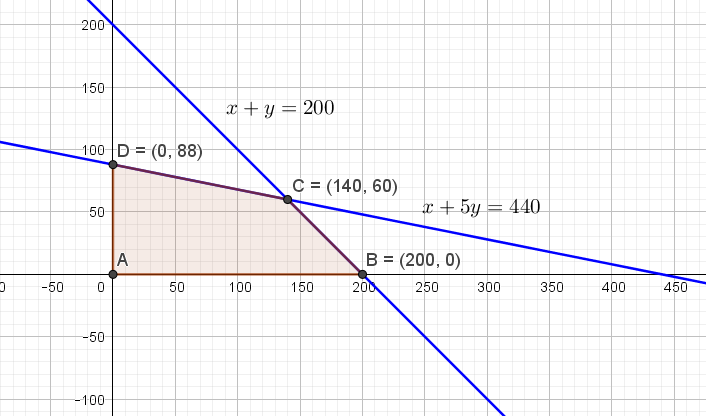
Daerah yang diarsir merupakan daerah penyelesaian dengan tiga titik pojok, yaitu titik , dan .
Untuk mencari koordinat titik , carilah penyelesaian dari karena merupakan titik potong kedua garis itu.
Uji ketiga titik pojok pada fungsi objektif .
Dari tabel di atas, diketahui bahwa keuntungan maksimum yang dapat dicapai sebesar Rp260.000,00 (Jawaban C)
Fungsi objektif:
Gambarkan sistem pertidaksamaan linear di atas ke dalam sistem koordinat.

Daerah yang diarsir merupakan daerah penyelesaian dengan tiga titik pojok, yaitu titik , dan .
Untuk mencari koordinat titik , carilah penyelesaian dari karena merupakan titik potong kedua garis itu.
Uji ketiga titik pojok pada fungsi objektif .
Dari tabel di atas, diketahui bahwa keuntungan maksimum yang dapat dicapai sebesar Rp260.000,00 (Jawaban C)
2. Seorang anak diharuskan minum dua jenis tablet setiap hari. Tablet jenis I mengandung unit vitamin A dan unit vitamin B. Tablet jenis II mengandung unit vitamin A dan unit vitamin B. Dalam hari, anak tersebut memerlukan vitamin A dan unit vitamin B. Jika harga tablet I Rp4.000,00 per butir dan tablet II Rp8.000,00 per butir, maka pengeluaran minimum untuk pembelian tablet per hari adalah
A. Rp6.000,00 D. Rp20.000,00
B. Rp6.700,00 E. Rp22.000,00
C. Rp7.000,00
A. Rp6.000,00 D. Rp20.000,00
B. Rp6.700,00 E. Rp22.000,00
C. Rp7.000,00
Penyelesaian
Berdasarkan informasi yang diberikan pada soal, dapat disusun tabel berikut.
Dari tabel di atas, dapat disusun sistempertidaksamaan linear
yang merupakan kendala dari fungsi objektif .
Gambarkan grafik dari setiap pertidaksamaanlinear di atas pada koordinat Kartesius seperti berikut.

Daerah penyelesaiannya tampak pada gambar di atas (diwarna), dengan titik pojok , dan . Perhatikan bahwa koordinat titik dapat ditentukan dengan menggunakan metode penyelesaianSPLDV.
Selanjutnya, ujilah nilai optimum dari masing-masing titik pojok itu terhadap fungsi objektif dengan menggunakantabel seperti di bawah ini.
Berdasarkan tabel di atas, pengeluaran minimum untuk pembelian tablet per hari sesuai dengan persoalan tersebut adalah Rp20.000,00 (Jawaban D)
Dari tabel di atas, dapat disusun sistempertidaksamaan linear
yang merupakan kendala dari fungsi objektif .
Gambarkan grafik dari setiap pertidaksamaanlinear di atas pada koordinat Kartesius seperti berikut.

Daerah penyelesaiannya tampak pada gambar di atas (diwarna), dengan titik pojok , dan . Perhatikan bahwa koordinat titik dapat ditentukan dengan menggunakan metode penyelesaianSPLDV.
Selanjutnya, ujilah nilai optimum dari masing-masing titik pojok itu terhadap fungsi objektif dengan menggunakantabel seperti di bawah ini.
Berdasarkan tabel di atas, pengeluaran minimum untuk pembelian tablet per hari sesuai dengan persoalan tersebut adalah Rp20.000,00 (Jawaban D)

Komentar
Posting Komentar