Transformasi dapat diartikan sebagai perubahan. Sehingga, transformasi geometri dapat didefinisikan sebagai perpindahan benda dalam ruang lingkup geometri. Di bangku SMA, materi transformasi geometri diberikan saat kelas XII. Dalam pembahasan di halaman ini, penjabaran yang akan diuraikan meliputi translasi, refleksi, rotasi, dan dilatasi. Materi yang akan dibahas meliputi ilustrasi perubahan dan rumus transformasi geometri yang meliputi translasi, refleksi, rotasi, dilatasi.
Rumus pada transformasi geometri akan memudahkan sobat untuk menentukan hasil transformasi tanpa harus menggambarnya dalam bidang kartesius terlebih dahulu. Meskipun begitu, ilustrasi gambar tentang transformasi juga dapat memberikan tambahan pemahaman buat sobat idschool. Untuk itu, mari simak pembahasan mengenai translasi, refleksi, rotasi, dan dilatasi pada penjabaran materi di bawah.
Translasi (Pergeseran)
Materi pertama tentang rumus transformasi geometri yang akan dibahas adalah translasi (pergeseran). Translasi merupakan perubahan objek dengan cara menggeser objek dari satu posisi ke posisi lainnya dengan jarak tertentu. Penentuan hasil objek melalui translasi cukup mudah. Caranya hanya dengan menambahkan absis dan ordinat dengan jarak tertentu sesuai dengan ketentuan. Untuk lebih jelasnya mengenai proses translasi dapat dilihat pada gambar di bawah.

Refleksi (Pencerminan)
Pembahasan berikutnya adalah pencerminan atau yang lebih sering disebut dengan refleksi. Seperti halnya bayangan benda yang terbentuk dari sebuah cermin. Sebuah objek yang mengalami refleksi akan memiliki bayangan benda yang dihasilkan oleh sebuah cermin. Hasil dari refleksi dalam bidang kartesius tergantung sumbu yang menjadi cerminnya. Pembahasan materi refleksi yang akan diberikan ada tujuh jenis. Jenis-jenis tersebut antara lain adalah refleksi terhadap sumbu x, sumbu y, garis y = x, garis y = -x, titik O (0,0), garis x = h, dan garis y = k. Berikut ini adalah ringkasan daftar matriks transformasi pada refleksi/pencerminan.

Selanjutnya, mari perhatikan uraian matriks transformasi untuk setiap jenisnya.
Pencerminan terhadap sumbu x

Pencerminan Terhadap Sumbu y

Pencerminan terhadap Garis y = x

Pencerminan terhadap Garis y = – x

Pencerminan terhadap Titik Asal O(0,0)

Pencerminan terhadap Garis x = h

Pencerminan terhadap Garis y = k

Rotasi (Perputaran)
Rotasi atau perputaran merupakan perubahan kedudukan objek dengan cara diputar melalui pusat dan sudut tertentu. Besarnya rotasi dalam transformasi geometri sebesar  disepakati untuk arah yang berlawanan dengan arah jalan jarum jam. Jika arah perputaran rotasi suatu benda searah dengan jarum jam, maka sudut yang dibentuk adalah
disepakati untuk arah yang berlawanan dengan arah jalan jarum jam. Jika arah perputaran rotasi suatu benda searah dengan jarum jam, maka sudut yang dibentuk adalah  . Hasil rotasi suatu objek tergantung dari pusat dan besar sudut rotasi. Perhatikan perubahan letak kedudukan segitiga yang diputar sebesar
. Hasil rotasi suatu objek tergantung dari pusat dan besar sudut rotasi. Perhatikan perubahan letak kedudukan segitiga yang diputar sebesar  dengan pusat
dengan pusat  pada gambar di bawah.
pada gambar di bawah.

Mendapatkan hasil rotasi dengan cara menggambarnya terlebih dahulu akan sangat tidak efektif. Ada cara lain yang dapat digunakan untuk menentukan hasil objek hasil rotasi, yaitu dengan menggunakan rumus transformasi geometri untuk rotasi. Simak lebih lanjut rumusnya pada pembahasan di bawah.
Rotasi dengan Pusat  sebesar
sebesar 

Rotasi dengan Pusat (m,n) sebesar 

Rotasi dengan pusat (0,0) sebesar  kemudian sebesar
kemudian sebesar 

Rotasi dengan pusat P(m,n) sebesar  kemudian sebesar
kemudian sebesar 

Dilatasi
Dilatasi disebut juga dengan perbesaran atau pengecilan suatu objek. Jika transformasi pada translasi, refleksi, dan rotasi hanya mengubah posisi benda, maka dilatasi melakukan transformasi geometri dengan merubah ukuran benda. Ukuran benda dapat menjadi lebih besar atau lebih kecil. Perubahan ini bergantung pada skala yang menjadi faktor pengalinya. Rumus dalam dilatasi ada dua, yang dibedakan berdasarkan pusatnya. Selanjutnya perhatikan uraian rumus untuk transformasi geometri pada dilatasi di bawah.
Dilatasi titik  terhadap pusat O(0,0) dengan faktor skala m
terhadap pusat O(0,0) dengan faktor skala m
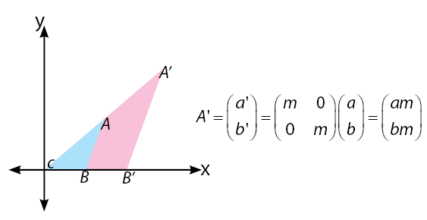
Dilatasi titik  terhadap pusat P(k,l) dengan faktor skala m
terhadap pusat P(k,l) dengan faktor skala m

Contoh Soal dan Pembahasan
Contoh Soal Translasi
Hasil translasi itik oleh
oleh  dilanjutkan dengan
dilanjutkan dengan  menghasilkan titik
menghasilkan titik  . Komponen translasi dari
. Komponen translasi dari  yang sesuai adalah ….
yang sesuai adalah ….
Hasil translasi itik
Pembahasan:
Misalkan
Misalkan
Diketahui:
Maka
Perhatikan proses translasi berikut.

Mencari nilai a:
Mencari nilai b:
Jadi, nilai translasi dari  adalah
adalah
Jawaban: B
Contoh Soal dan Pembahasan Transformasi Geometri Refleksi
Persamaan garis  karena refleksi terhadap garis y = x, dilanjutkan oleh transformasi yang bersesuaian dengan matriks
karena refleksi terhadap garis y = x, dilanjutkan oleh transformasi yang bersesuaian dengan matriks  adalah ….
adalah ….
Pembahasan:
Pencerminan terhadap garis adalah:
adalah:

Berdasarkan rumus di atas, dapat diperoleh kesimpulan bahwa dan
dan  . Substitusikan nilai tersebut pada persamaan
. Substitusikan nilai tersebut pada persamaan  sehingga diperoleh persamaan berikut.
sehingga diperoleh persamaan berikut.
Pencerminan terhadap garis

Berdasarkan rumus di atas, dapat diperoleh kesimpulan bahwa
Selanjutnya adalah transformasi yang bersesuaian dengan matriks  :
:
Sehingga, diperoleh dua persamaan berikut.
Mencari nilai  :
:


Mencari nilai  :
:


Subtitusi hasil  dan
dan  di atas pada persamaan – x’ + 3y’- 11 = 0:
di atas pada persamaan – x’ + 3y’- 11 = 0:
Jadi, hasil akhir transformasi dari persamaan 3x – y – 11 = 0 adalah 2x – 7y + 11 = 0.
Jawaban: E
Contoh Soal dan Pembahasan Transformasi Geometri Rotasi
Hasil pencerminan garis x – 2y -2 = 0 terhadap sumbu y dan kemudian diputar dengan![Rendered by QuickLaTeX.com R\left[ O(0,0), \; 90^{o}\right]](https://idschool.net/wp-content/ql-cache/quicklatex.com-92fb231bb1e68676a8abe126f1ba1697_l3.svg) adalah ….
adalah ….
Hasil pencerminan garis x – 2y -2 = 0 terhadap sumbu y dan kemudian diputar dengan
Pembahasan:
Hasil transformasi pencerminan terhadap sumbu y adalah:

Hasil transformasi pencerminan terhadap sumbu y adalah:

Sehingga diperoleh x’ = – x dan y’ = y, selanjutnya substitusikan kedua nilai yang diperoleh pada persamaan x – 2y – 2 = 0.
Transformasi selanjutnya adalah rotasi sebesar  yang berpusat di
yang berpusat di  :
:
Substitusi nilai x’ = y’’ dan y’ = – x’’ pada persamaan -x’ – 2y’ – 2 = 0, akan diperoleh
Jadi, hasil pencerminan garis x – 2y -2 = 0 terhadap sumbu y dan kemudian diputar dengan ![Rendered by QuickLaTeX.com R[ O, 90^{o}]](https://idschool.net/wp-content/ql-cache/quicklatex.com-36b3be837e217dbd4cd6cace918dc1f4_l3.svg) adalah 2x – y + 2 = 0.
adalah 2x – y + 2 = 0.
Jawaban: D
Contoh Soal dan Pembahasan Transformasi Geometri Dilatasi
Dilatasi yang berpusat di titik (3, 1) dengan faktor skala 3, memetakan titik (5, b) ke titik (a, 10). Maka nilai a – b adalah ….
Dilatasi yang berpusat di titik (3, 1) dengan faktor skala 3, memetakan titik (5, b) ke titik (a, 10). Maka nilai a – b adalah ….
Pembahasan:
Dilatasi dengan pusat (3, 1) dengan faktor skala 3 akan menghasilkan matriks transformasi berikut.
Dilatasi dengan pusat (3, 1) dengan faktor skala 3 akan menghasilkan matriks transformasi berikut.
Sehingga diperoleh nilai
Jadi, nilai  .
.
Jawaban: C
Jawaban: C

Komentar
Posting Komentar